【統計学入門】統計学とは何か？ 記述・推測統計、ベイズ統計との違いも解説！

統計学とは？ 実は2種類に分けられる！

統計学とは何か？
この問いに一言で答えるとしたら次のようになります。

これだけ読んでも、わかるようなわからないような抽象的な定義ですね。
（一言って言ったのに、2つの並列の要素を並べてますし、、、）

実は、統計学は2種類の分野に分けることができるんです。
それが、「記述統計学」と「推測統計学」です！

記述統計学と推測統計学

それぞれどのような学問かというと、、

記述統計学 ： ある程度以上の数のバラツキのあるデータの性質を調べる学問
推測統計学 ： 「大きなデータ」から「一部を抜き取ったデータ」の性質を調べることで、元の大きなデータの性質を推測する学問

実は、最初に述べた統計学の説明が長くなってしまったのは、これら2つの統計学の説明を結合したものだったからです！

記述統計学に関しては、おそらくみなさんも日頃使っているかと思います。
例えば、
「全科目のテストの点数から全体の平均値を出す」
といった場合は記述統計学をしていると言えます。

一方で、推測統計学については少しわかりづらいかもしれません。
例えば、
「友達5人で数学のテストの点数を見比べて、クラス全体の平均点を推測する」
といった時は、推測統計学の考え方に近いです。

ちなみに、上の推測統計学の定義に書いていた「大きなデータ」のことを統計学では「母集団」と呼び、
「(大きなデータから)一部を抜き取ったデータ」のことを「標本」と呼びます。

先ほどの数学のテストの例だと、

大きなデータ ： クラス全体の数学の点数
一部を抜き取ったデータ ： 友達５人の数学の点数
大きなデータの性質 ： クラス全体の平均点

が推測統計学の定義に対応します。

記述統計学と推測統計学の関係

まとめると、記述統計学と推測統計学の関係は以下のようになります。

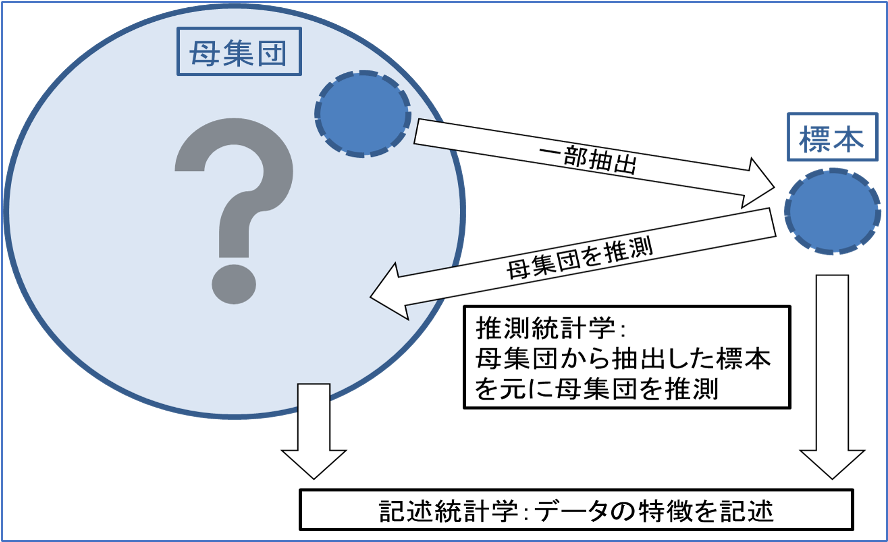
このように、推測統計学は「母集団」から抽出した一部のデータである「標本」を使用して、母集団がどのような集団であるかを推測します。
ここでの推測するものとは例えば、母集団の平均や分散やパラメータといったものを指しています。

一方で、記述統計学は手元にあるデータがどのようなデータなのかを調べるだけなので、母集団や標本の考え方とは関係ないことが図からわかります。

ベイズ統計学

ここまで統計学は2つに分けられて、それは「記述統計学」「推測統計学」だと説明してきました。
しかし、実はもう一つ「ベイズ統計学」と呼ばれる学問があります。

そんなツッコミが聞こえてきそうですが、3つと言わなかったのは大きな理由があります。

それは、ここまで説明してきた統計学とベイズ統計学では全く考え方が異なるため、同じ学問として扱うのは難しいからです。

実はここまで説明してきた、そしてこれから学ぶ統計学は、頻度論と呼ばれる考え方に基づいています。
一方で、ベイズ統計学はベイズ論という考え方に基づいているため、アプローチが異なります。

そのため、一般的な統計学の本ではベイズ統計学について深く記述されておらず、個別に専門書が出版されています。

ベイズ統計学は近年データサイエンスの中でも特に注目されている分野の一つなので、概要くらいは知っておくと良いでしょう！

ちなみに、統計検定でもベイズの問題は近年多く出題されていることからも注目度の高さが窺えます。

ベイズ統計学とは？

ベイズ統計学は、数学者トーマス・ベイズによって提唱された「ベイズの定理」を中心とした、ベイズ的な考え方によって展開される統計学です。

「ベイズの定理」「ベイズ的な考え方」新しい言葉が2つ出てきましたね。順に解説していきます！

高校数学では、事象\(A,B\)の条件付き確率は、

$$ P(A|B) = \frac{P(A\cap B)}{P(B)} \tag{1}$$

と書いていました。
これだけだと、ただの条件付き確率なので、
同じく高校数学の「確率の乗法定理」という定理を(1)式に使います。

まず、確率の乗法定理は

$$ P(A \cap B) = P(A)P(B|A) \tag{2} $$

で表されます。
これを(1)の条件付き確率に適用すると、

$$ P(A|B) = \frac{P(A)P(B|A)}{P(B)} \tag{3}$$

となり、(3)式がベイズの定理と呼ばれるものです。

この簡単そうに見える定理に重要な事実が隠されています。
それは左辺の\( P(A|B) \)と\( P(B|A) \)の文字が逆転していること、つまり因果が逆転しており、ある結果からその結果の原因の確率を求められることを示しています。

このことから、ベイズの定理は原因の確率を求める定理とも呼ばれており、この重要な性質を持っていることでベイズの定理が多くのビジネスで応用され、ベイズ統計学が注目されています。

ベイズ的な考え方？ 統計学とベイズ統計学の違い

(※ ここでは、パラメータという用語が出てくるので、ピンとこない方は読み飛ばしてもらっても構いません。)

続いて、「ベイズ的考え方」とは何か？について解説します。

先ほど、多くの人が学んでいる所謂統計学と呼ばれている学問は頻度論という考え方に基づいていると言い、一方でベイズ統計学はベイズ論という考え方に基づいていると言いました。

これらの考え方の違いを理解することで、ベイズ論つまりベイズ的考え方が何かが見えてきます。

頻度論は「データは真のパラメータから発生している」という考え方、つまり「データはパラメータによって決定された確率分布から発生される」と考えられています。
頻度論ではこの考え方に基づき、真のパラメータを推定するための方法が様々提案され、それを多くの人は学んでいます。

一方で、ベイズ論・ベイズ的考え方では「データこそ真実であり、ばらつくのはパラメータである」という頻度論と全く逆の考え方を持っています。
なので、パラメータが確率分布を持っており、スタンダードな統計学を学んだ人を混乱させることが多々あります。

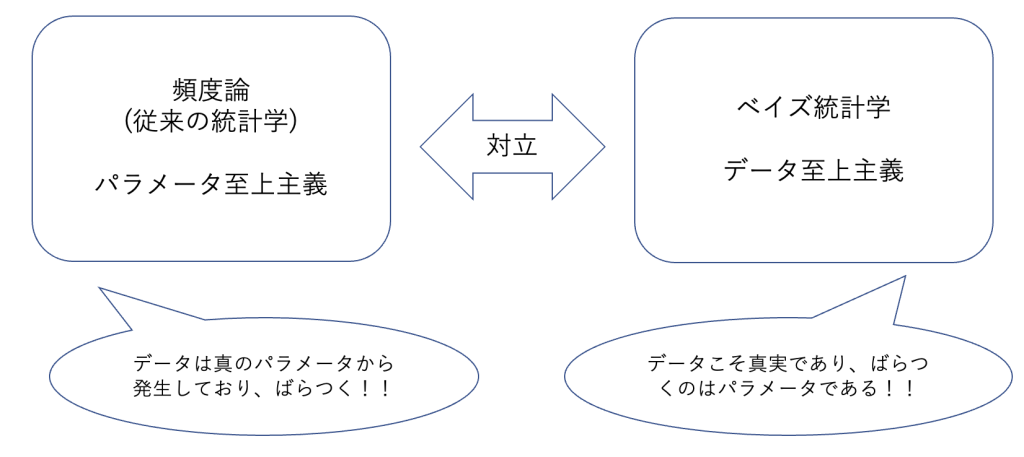
このように全く逆の考え方のため、従来の統計学には含まれず違う学問として学ぶことが多いわけです。

終わりに：データサイエンスは面白い！

初心者こそデータサイエンスをがむしゃらに勉強するのではなく、データサイエンスの各要素（本ページだと統計学）全体像を掴み自分がデータサイエンスで何を実現するために学んでいるか把握することで、知識の定着度や理解度が速くすることができます。

以下の記事では、一人前のデータサイエンティストになるまでのロードマップについて紹介しています。
これからデータサイエンスを学ぼうとしている方はよろしければ、こちらもご覧ください！

また、今大学生の方で新卒でデータサイエンティストを志望している方向けに、
僕がデータサインエンティストになるために就活をしている中で気づいたことをまとめた記事も載せています。
参考になると思うので、こちらも併せてご覧ください。